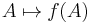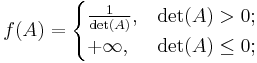Polyconvex function

In mathematics, the notion of polyconvexity is a generalization of the notion of convexity for functions defined on spaces of matrices. Let M_m×n(K) denote the space of all m × n matrices over the field K, which may be either the real numbers R, or the complex numbers C. A function f : M_m×n(K) → R ∪ {±∞} is said to be polyconvex if

$A \mapsto f(A)$

can be written as a convex function of the p × p subdeterminants of A, for 1 ≤ p ≤ min{m, n}.

Polyconvexity is a weaker property than convexity. For example, the function f given by

$f(A) = \begin{cases} \frac1{\det (A)}, & \det (A) > 0; \\ %2B \infty, & \det (A) \leq 0; \end{cases}$

is polyconvex but not convex.

References

Renardy, Michael and Rogers, Robert C. (2004). An introduction to partial differential equations. Texts in Applied Mathematics 13 (Second edition ed.). New York: Springer-Verlag. pp. 353. ISBN 0-387-00444-0. (Definition 9.25)